An Introduction To Valid Post Selection Inference
As a mathematician, I have grown used to using statistical concepts such as linear regression to describe the "effects" of random variables. Essentially, a large part of my undergraduate degree revolves around analysing data and variables to try and find the "useful" information which they provide. In essence, this is what the topic of statistics is: we are given data which represents "random variables: - things that we can observe and which change randomly like the price of a stock in finance, or a gene within the human body. In order to make valid inferences (make conclusions) from these phenomena, we must consider so called "parameters". These are the things which statisticians wish to make conclusions from, and examples include the mean (the average result), median (the middle result) and mode (the most common result). The method to analyse these "parameters" is to observe the data (the random variables) and use estimates for these values (which we call an estimator) to try and form reasonable conclusions. Obviously, the more data we have, the more similar we can make these estimates to the real world processes we are trying to model - taking the heights of every person on the planet would give a much more accurate estimate for the mean height of a human than if we just took the height of the first two people we met. Within the subject of mathematics, such concepts are well understood. Thus we can usually create 'good' models which accurately describe what we are measuring when we have lots of data (random variables) and only a few parameters. However, the case where we have many parameters and only few random variables (where we want more conclusions than we have data and results) is very misunderstood and complex, and in fact many of our classical statistical concepts do not work here at all. This is what my research aims to examine, and I am currently attempting to delve into this unknown realm of statistics by examining a technique called 'Valid Post Selection Inference'.
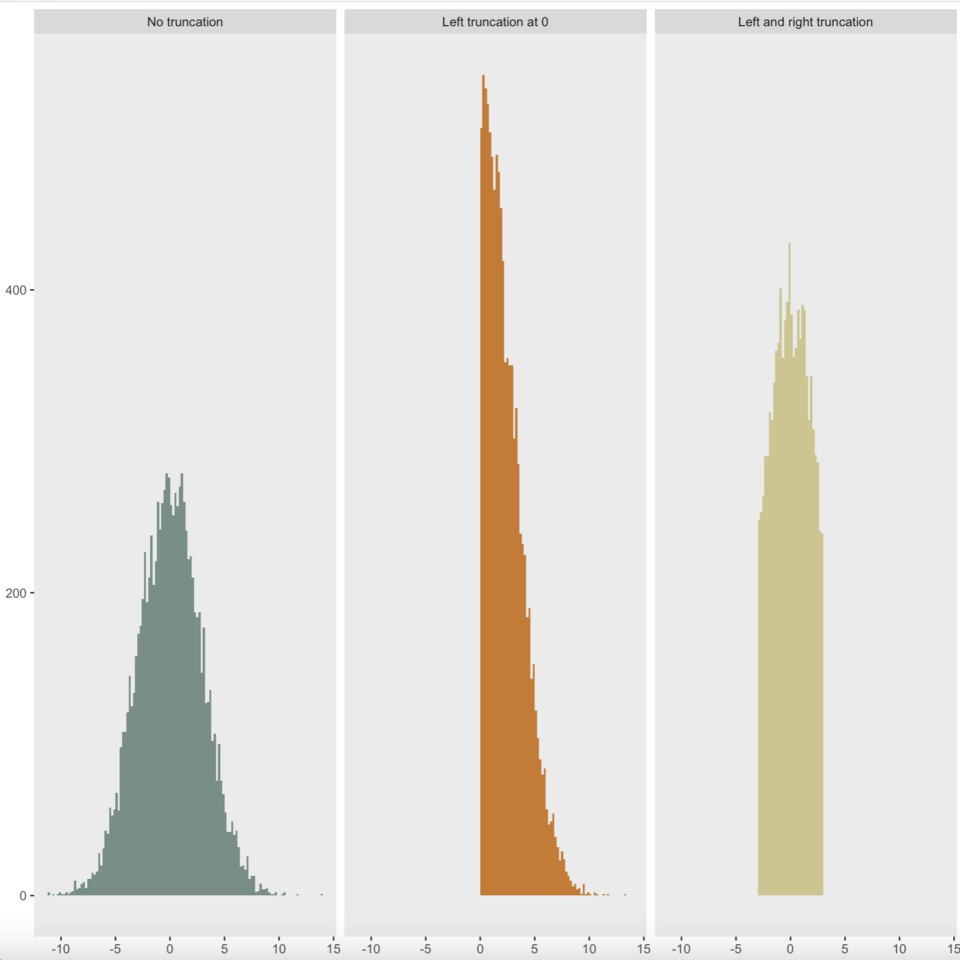
The general concept of 'Valid Post Selection Inference' is that we cut down the number of variables to only include the ones which have the biggest impact on our results, and which hence will more accurately represent our phenomena. We do this via a method called the 'Lasso', and I have implemented this into my work this week by using the package 'lars' in the programming language R to select the variables I wish to use. The method and algorithm I use is one described in Tibshirani (2013). A snapshot of one of the plots which I have created using the package to aid my understanding is shown below. this plot represents the effect the penalty parameter in the lasso has on the mean-square error, two vital statistical concepts:
I experimented with various datasets, and used the algorithm on a very useful set of data detailing the key variations in diamonds to produce the following plot:
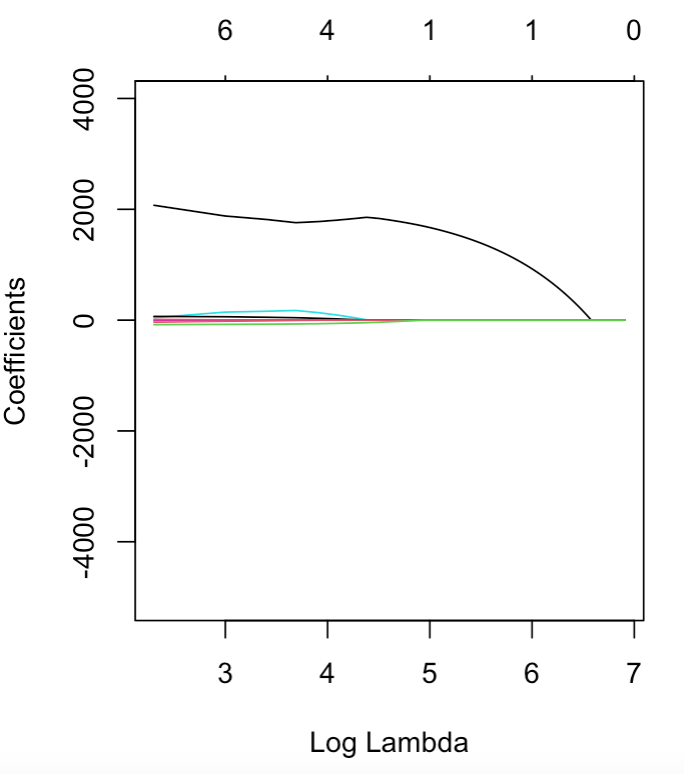
This plot is a fantastic illustrative example, as it shows that one variable (the black line) has a much larger affect on the overall result than the rest of the data.
Following this exploration into the lasso, I switched to a more mathematical methodology by following the processes and methods outlined in Lee et al. (2016) to show how to find a confidence interval. This article works in the known case where the number of variables is less than the number of parameters, but uses methods which will generalise to the more difficult case where the number of parameters is greater than the number of variables, and hence is a great article with which to start my research. The article starts by identifying the problems which the lasso method has - namely that if we are removing variables from our data, then from a mathematical viewpoint, we have no idea which variables will be removed. Hence from a theoretical point of view, we must consider every possibility available, and hence consider each combination of variables we can remove separately. This obviously takes a lot longer than just considering the one scenario, and hence is impractical, and if the data is large enough (think millions of variables) then the manipulation of the data is physically impossible due to the amount of time and computing power which would be required. However, this paper introduces concept of conditioning our events on the actual model we choose (the choice of variables we remove). Mathematically, this is a big difference and the theory is addressed throughout the rest of the paper, but practically (and much more importantly) this makes the mathematics and calculations a lot easier and is hence a fantastic concept.
The paper continues to develop the theory of this conditioning, and explains how we can reduce our choice of model to the affine relation : AY ≤ b (note this is called an affine relation as the quantity A is a matrix, whilst b and Y are vectors, so sadly this equality is not as easy to solve as it first appears). We use this relation to further understand our given model, and eventually we come to the conclusion that our conditioned variables have a 'Truncated Normal' distribution. This is a regular normal distribution which has (loosely speaking) been truncated, or sliced at specific values. Examples of various truncated normal distributions are shown in the image (coded in R) below:
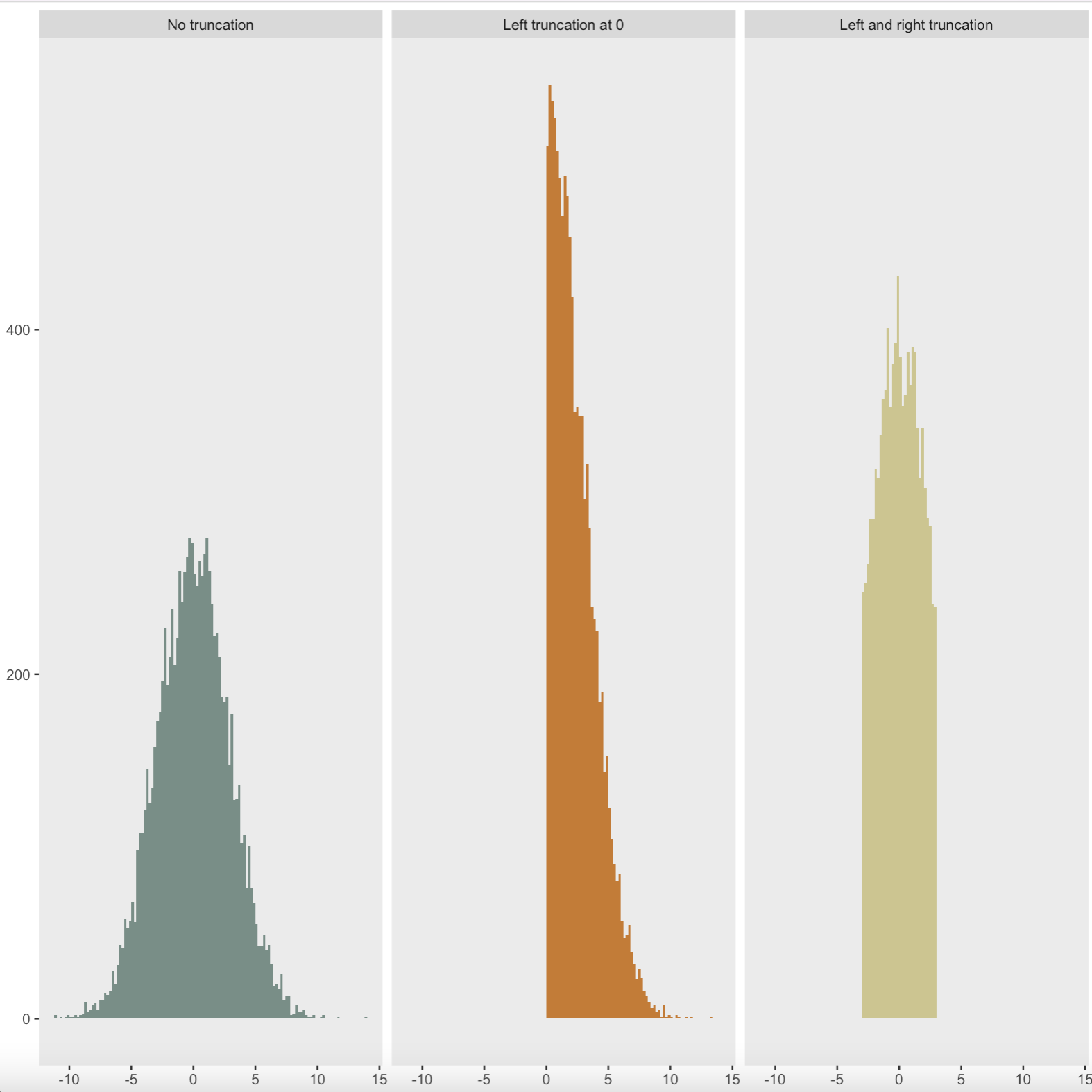
From a mathematical view, this is the key piece of theory which we needed, as this allows us to make confidence intervals and other important statistical inferences using our model. An example confidence interval (in general terms) is shown below:

This concluded the results of this paper and provides a basis for generalising my work to the more complex situation where the number of parameters outnumbers the number of variables as my research develops.
References
Tibshirani (2013) - The lasso problem and uniqueness. Electron. J. Stat. 7 1456–1490. MR3066375






Please sign in
If you are a registered user on Laidlaw Scholars Network, please sign in