Developing analog systems for the interior of blackholes
In modern science, there are many areas where experimental verification is far beyond our technological capabilities. One way in which physicists have attempted to probe these areas is by producing systems of a similar scale to the world we live in, which act very similarly to the target systems. One such successful system is the modelling of the surface of blackholes or more specifically, their Hawking radiation: the production of a pair of particles on a surface, with one escaping the ‘blackhole’ and one being trapped. Since, by definition, no potential measurement device which reaches the event horizon could ever be recovered, this sort of effect would be virtually impossible to measure experimentally. This has been done through various methods, for example using sound (sonic) to recreate the same effect.
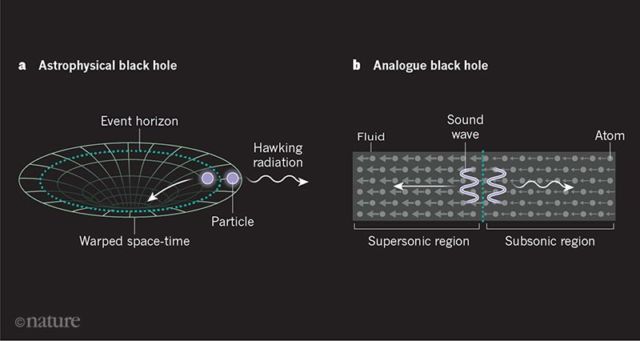
My project is to produce a similar analogue but for a system that may model the conditions inside a blackhole.
The system that I am investigating is known as Dirac solitons, a pair of electrically neutral particles bound together by their own strong gravitational attraction; but which are prevented from collapsing into a point by the uncertainty principle. These were first explored by Finster, Smoller and Yau (FSY) in their 1999 paper. This system is on the boundary of general relativity and quantum mechanics (although the gravitational field is not quantised.) We have not yet found a theory, known as a grand unification theory (GUT), bridging these two areas of physics. This makes studying simplified systems (such as FSY) potentially very useful for developing such a GUT, which if discovered could be the greatest ever success of physics.
The difficulty with testing a theory derived through FSY is that these particles are at a much smaller scale (at an order of magnitude equivalent to the Plank length ~1.6*10^-35) than we can experimentally probe now, or in the foreseeable future.
The first candidate for creating an analogue is using a graphene sheet as the spacetime and charges as the particles. This is attractive as it is a very physical and intuitive system which, if it produces accurate results, could also be very useful for teaching and developing intuition. The main issue is that it is a very stiff material, so if the values which it produces are of incorrect scale, it is too inflexible to manipulate.
The second candidate is using a superconducting circuit, with both the particles and framework being different charges. However, this is a far less intuitive candidate. While mathematically equivalent, it is physically very different. However, this type of setup has been shown to be capable of producing the kind of back-action, of the particles affecting spacetime itself, which is required by the FSY system (but is not present in Hawking radiation analogues) and it is inherently quantum mechanical.
Should the previous example not work, another possibility is to use a non-linear optical device and simulate the particles as photons in a cavity. This is a compelling candidate as it is very quantum mechanical, but also is an area in which there is an enormous body of research available. However, we are presented with various challenges with this technique, primarily the fact that there is no photon-photon interaction, so various apparatuses would need to be used to remedy this.
I have spent the last few weeks doing background learning in general relativity and relativistic quantum mechanics; have worked through the FSY paper to understand the mathematics behind the paper; and have begun trying to understand how applicable and practical these potential candidates are. I will be looking to continue this study and come up with a potential candidate which I will hopefully be able to test next summer.
I would like to thank my supervisor, Dr Chris Hooley, for the opportunity to work with him and explore this fascinating area of physics. I would also like to thank the entire Laidlaw team, especially Lord Laidlaw himself, who made the Laidlaw Scholarship program possible.




Please sign in
If you are a registered user on Laidlaw Scholars Network, please sign in