Snail’s pace: conchology and 200 years of mathematical biology

The first part of my research has focused on gaining a familiarity with mathematical models of shell growth and form, in relation to a (delayed due to travel restrictions) project on land snail diversity in the Galapagos Islands. Reading revealed a surprisingly substantial body of work on the peculiarities of molluscan form, more than two hundred years in the making. In this post, I outline a small selection of the key ideas and contributors to the mathematical descriptions of nature’s spira mirabilis.
So far as I can ascertain, it was René Antoine Ferchault de Réaumur who first mathematicised conchology, back in 17091. A mathematician and physicist by education, Reaumur applied himself to a great many lines of scientific inquiry: steel, birds’ nests, beehives, artificial incubation, and a multitude of entomological subjects at various times received his attention2. Yet after Reaumur’s preliminary treatment, it appears that precious little mathematics was visited on the molluscs.
Then, after an interlude of 129 years, Henry Moseley published a description of the appearance of the logarithmic spiral in the molluscan shell, alongside formulae for determining the centre of mass, area, and volume of such a shell3.
In short, what Moseley recognised (and D’Arcy Wentworth Thompson subsequently popularised4) is the notion that many shells can be simply described in terms of a centreline curve and a generating curve, in which the centreline curve closely approximates a helicospiral, the three-dimensional equivalent of the logarithmic spiral. The latter is also termed the equiangular spiral, since a radial line from the origin has the same angle of intersection with the spiral, regardless of the position of the radial line5. In other words, the spiral is gnomonic: its form is preserved through an increase in the angle of revolution. Practically, this is intuitive: we expect a juvenile mollusc of a given species (excepting ontogenetic changes to ornamentation or aperture) to adhere to the same geometry as a mature individual. In other words, the accretive growth of a shell preserves its ‘shape’.
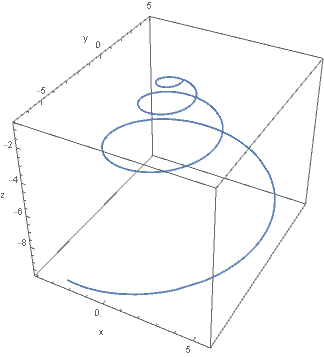
Above: Helicospiral centreline curve
The generating curve, to an approximation, is the shape of the aperture – a cross-section, which is centred on the centreline curve and revolves about the coiling axis to describe the two-dimensional surface of the shell. In the most basic case, we may assume the generating curve to be circular, to produce a fairly plausible model as shown in the image below.

By taking certain measurements of the shell and calculating ratios of length, parameters specifying the centreline and generating curve can be found and used to produce a model. However, this descriptive method, while satisfying, clearly has limited explanatory power. A parametric description does not tell us anything about how the shell came to take a particular form, nor why that particular form is advantageous (or otherwise).
Enter David M. Raup, who, following Thomson’s classic On Growth and Form, applied the descriptive model to comparative morphology, and explored the notion of developmental constraint (which is even now an area of inquiry in modern evolutionary developmental biology). After a preliminary discussion of shell morphology in 19611, Raup identified the concept of the morphospace as a convenient tool for investigating the diversity of shell forms6. Simply speaking, the morphospace is the three-dimensional region spanned by the expansion rate (how quickly the cross-section grows), translation rate (determining the planarity of the shell) and generating curve displacement, which is populated by fossil and extant morphologies.
Raup noticed that extinct and extant species occupy only a small corner of the morphospace, paving the way to the question: ‘Do the relatively unused regions represent physiologically impossible shell forms or has the evolution of these taxa simply not had sufficient time in which to populate the entire block?’6 In other words, what physical constraints, if any, are at play in the development of mollusc diversity?
Raup was an advocate of the potential of precise geometric studies to reveal relationships between taxa, yet explicitly noted several drawbacks of this approach. In particular, ontogenetic changes (variations in growth occurring at specific times in an organism’s development) such as variation in expansion rate or modification of the aperture, mean that the final morphology can depart significantly from the logarithmic model6. This variation, coupled with significant phenotypic plasticity7, means that the resolving power of the geometric approach is limited.
Out of the limited predictive power of the descriptive model has sprung a complementary approach: the accretive growth model, used to great effect by Chirat, Moulton and Goriely8,9,10 to detail a mechanical hypothesis for the emergence of ornamentation (think spires, folds and ribbing patterns). Instead of specifying an entire shell shape in terms of a small set of parameters, the accretive model utilizes a field of growth vectors defined on the generating curve, within the Frenet frame. Integration of the growth vectors then simulates the gradual process of calcium carbonate crystallization to produce the shell form.
The accretive model is flexible, in that the effects of varying the orientation of the growth vectors can be visualized. Indeed, with this approach, it is simple to simulate even the ontogenetic changes at the aperture lip using a step function ‘switch’ and a matrix of rotation about the tangent vector of the Frenet frame, an approach which I imagined and implemented in this project, and which was previously lacking from research designed simply to recreate the shell form (I would need to expand the model into mechanical considerations to make it physically relevant).
The particular success of the accretive method, however, lies in testing hypotheses. For example, Moulton, Goriely and Chirat demonstrated that elastic deformation of the mantle (the living part of the mollusc, the edge of which is the location of shell deposition), resulting from a mismatch of growth rates of the mantle and shell, produces very closely the patterns of ornamentation observed in many marine species11.
Though evidently informative, this work is not conclusive. There may be multiple models consistent with the observed ornamentation. Furthermore, the mechanical approach, while offering a possible explanation of the ‘how’ question of shell growth, does not presume to account for the ‘why’ (Why should these features be present at all?), nor the long list of superordinate how’s, dealing with the whys and wherefores of evolution and ecological niche. Mathematical approaches must progress hand in hand with empirical studies in the field and laboratory if the origin of diversity in shell form is to be understood.
In the meantime, even Raup’s geometric approach may shed some light on molluscan diversity. New Zealand is home to an intriguing array of predatory snails, including the stunning Powelliphanta, ground-dwelling hunters the size of ramekins which slurp worms like linguine12. Then there is the flax snail Placostylus hongi, whose high-spired shell with small angle of inclination is so distinct from the almost planispiral configuration of Powelliphanta.
Among all the disk-like endemic ground dwellers, the shell of Placostylus, which resides in vegetation while a small juvenile size permits, sticks out like an eyestalk. Goodfriend noted a putative correlation between degree of planarity and resting surface inclination among the terrestrial gastropods13, but the generality of this suggestion, still less an explanation, is unknown. Is there a mechanical constraint which determines the supposed relationship between translocation rate and surface inclination? Geometry may yet lend a helping hand.
- Raup, D.M. (1961). The geometry of coiling in gastropods. Proc. Natl. Acad. Sci. USA 47(4), pp. 602–609
- Wikisource contributors. (1911). Réaumur, René Antoine Ferchault de. Encyclopædia Britannica / Wikisource . Available at: https://en.wikisource.org/w/index.php?title=1911_Encyclop%C3%A6dia_Britannica/R%C3%A9aumur,_Ren%C3%A9_Antoine_Ferchault_de&oldid=9530328. Accessed July 3, 2020.
- Moseley, H. (1838). On the geometrical forms of turbinated and discoid shells. Philosophical Transactions of the Royal Society of London, pp. 351–370
- Thompson, D.A.W. (1952). On Growth and Form. University Press, Cambridge
- Mukhopadhyay, U. (2004). Logarithmic Spiral – A Splendid Curve. Resonance, pp. 39-45
- Raup, D.M. (1966). Geometric Analysis of Shell Coiling: General Problems. Journal of Paleontology 40 (5), pp. 1178-1190
- Brook, F.J. & McArdle, B.H. (1999) Morphological variation, biogeography and local extinction of the northern New Zealand landsnail Placostylus hongi (Gastropoda: Bulimulidae), Journal of the Royal Society of New Zealand, 29 (4), pp. 407-434
- Moulton, D.E., Goriely, A. & Chirat, R. (2015) The morpho-mechanical basis of ammonite form. Journal of Theoretical Biology, 364 pp. 220-230
- Erlich, A., Moulton, D.E., Goriely, A., & Chirat, R. (2016). Morphomechanics and Developmental Constraints in the Evolution of Ammonites Shell Form. J Exp Zool B Mol Dev Evol. 326(7) pp. 437-450.
- Goriely, A. (2017). The Mathematics and Mechanics of Biological Growth. Springer-Verlag, New York.
- Chirat, R., Moulton, D.E. & Goriely, A. (2013). Mechanical basis of morphogenesis and convergent evolution of spiny seashells. Proceedings of the National Academy of Sciences,110 (15) pp. 6015-6020
- Paddy Ryan. Snails and slugs - Flax snails, giant snails and veined slugs, Te Ara - the Encyclopedia of New Zealand, http://www.TeAra.govt.nz/en/snails-and-slugs/page-2
- Goodfriend G. A. (1986) Variation in land-snail shell form and size and its causes – a Review. Systematic Zoology 35 pp. 204–223



Please sign in
If you are a registered user on Laidlaw Scholars Network, please sign in