Machines Really Think?

So we live in a world where machines think. Not scary at all. Well that’s definitely something. How the hell did we get here? We have computers that recognise faces, recognise and translate speech, and keep that Nigerian Prince in your spam emails for you! So what the hell is going on? What makes this ‘thing’ made out of transistors (which deserve it’s own blog) and other components so smart? Well, I think for a start, we can talk about Neural Networks.
Background
Neural comes from the word neuron, which is just a nerve cell. These little guys do a lot. I mean, A LOT. From the feeling you get when you taste that beautiful Friday cocktail you’ve been thinking about since Monday, to the pain you feel when you hit your toe on the corner of your bed. How do they do all this? The way we should achieve most things. Together. We have up to 10^11 neurons in our brain, all interconnected, receiving inputs and sending outputs, all so that we can think, learn and memorise things. This is the basis of Artificial Neural Networks.
Structure
This is a simple neural network structure. It consists of three layers (from right to left): the input layer, the hidden layer (not really hidden is it?), and the output layer. I’ve named the neurons to help out when explaining.
Essentially, one should think of a neuron as a thing that holds a number between 1 and 0. We’ll call this number an activation. The number’s closeness to 0 or 1 means something to the whole system e.g. the brightness of a pixel where 0 is black and 1 is white. Neurons are connected to each other by synapses, but let’s call them lines because , um, five letters are better than eight? These lines have a certain weight that accompanies it. Think of this as a measure of how seriously the information that the line is carrying from one neuron is taken by the receiving neuron.
How do they work?
Let’s assume the neural network’s goal is to learn how to identify the handwritten numbers: 1, 2 and 3. A number is written, scanned and fed to the network's input layer. Ideally, each neuron in the input layer takes a third of the space on the scanned photo. Something like this:
.jpg)
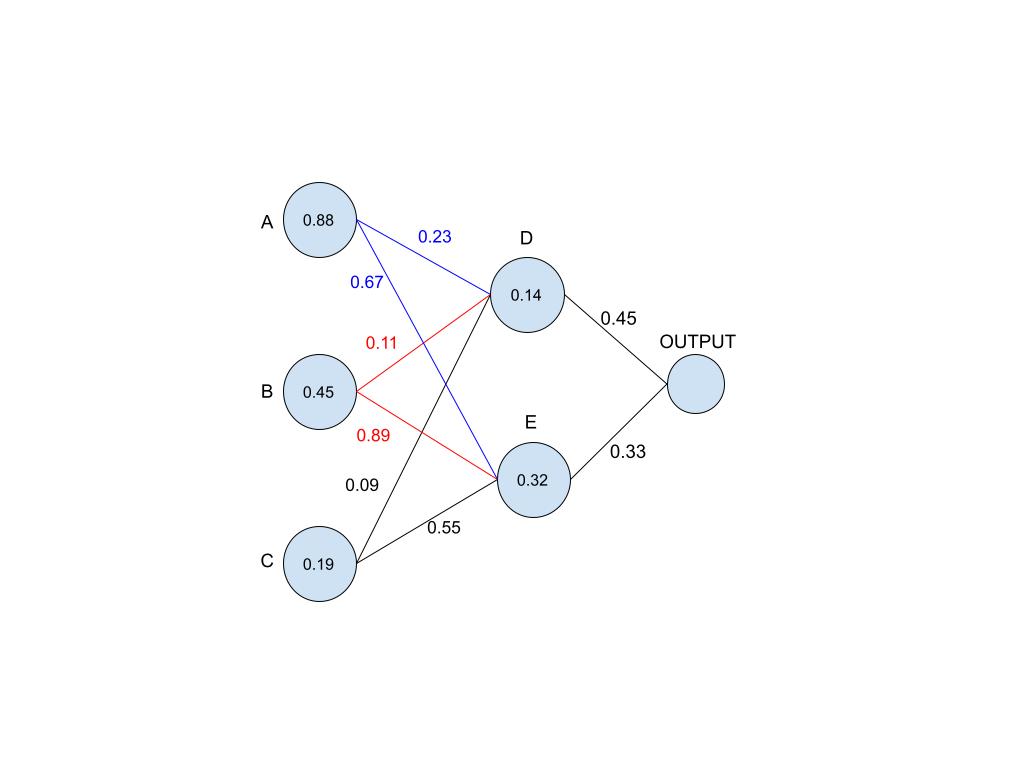
The neurons then calculate the area covered by the number in their respective sections and give output a number between 1 and 0, as indicated by the numbers inside the circles (A = 0.88, B = 0.45, C = 0.19). In the next layer, let’s focus on neuron D. Neuron D receives inputs from A, B and C. However, the inputs are not proportional. They are affected by the weights on the lines connecting them. Each input is multiplied by the weight on it’s line and then added at the end. So neuron D would receive something like this: A (0.88 * 0.23) + B (0.45 * 0.11) + C (0.19 * 0.09).
Don’t worry, I’ll do that maths for you. 0.269. But neuron D shows 0.14, am I really that bad at math? Each neuron also has a bias. Think of this as a measure of how much you need to give a neuron for it to be active. In this case we can loosely say the bias is the difference between the expected and actual result i.e. 0.269 - 0.14 = 0.129. This means if the neuron D receives a collective input of less than 0.129, it’ll remain at the 0 mark, because we can’t have anything below that.
Ok, let’s recap. A neuron is a number holder. Neurons are connected by lines. These lines have a weight that affects the number in the neurons in which it connects. The next layer of neurons receive the inputs (which have been weight affected) of all other neurons in the previous layer, add them up and then subtract (or add) a bias. After that the neuron is ready to send their output to the next layer. Good? I’ll assume that we are.
So this is a small system, and it’s very unlikely that the input received will be larger than one. However, a classic example of a neural network has 784 neurons in the input layer. The inputs will most definitely add up to more than 1, but we can’t have a number more than 1. Yeah that’s it, it can’t work. Thanks for wasting your time…
Ok ok, I’m sorry. I have separation anxiety so we’ll have to work through this. So we have a number that’s bigger than 1, and a thing that can’t take a number bigger than 1. Well, let’s just squeeze the damn thing! This large input is put through a magical box, called a sigmoid function. And this box makes sure that all the addition of all inputs into a neuron is less or equal to 1, and greater or equal to 0. A quick Google search will do you justice, I really don't want to bore you (and myself) with all the maths involved.
Great! So we have everything. And we can go from the input layer, to the hidden layer (which can be more than one), and finally we get an output that by the Harry Potter antics of the sigmoid function, is between 0 and 1. Then what?
Learning
It’s probably a good time to let you know that at this point the neural network is pretty trash at its job. The output you first get isn’t going to be accurate. We need it to learn, we need to teach it. When we were young, we didn’t automatically know which number was which. And when we learned that 7 looked like 7, some maniac came and put a small horizontal line through it (if you write your 7’s with a line through it, seek medical attention). We had to learn.
So how do we teach a neural network? You need test data. A lot of test data. And so you pass the scanned 3 (refer to the figure), and the ultimate output of the neural network is something that indicates a 5. Because this is test data, we know it’s a 3 and the network has gotten it wrong. So we have to, in a sense, pinch this network so that it understands it’s gotten the wrong thing. We need a cost for wrong answers.
This is precisely what it’s called. The cost function. There are many ways to make a cost function, and they get more complicated as they do better. An easy one to start with is taking the expected overall output, subtracting the actual overall output, and squaring it (just to deal with any negatives we might get). Now the bigger the cost function, the bigger the ‘pinch’ for the network. And so the network tries, like any child would, to stop getting pinched and just learn the stupid numbers! This is called backpropagation.
A neural network, in our case, has 3 variables. A neuron's activation, it’s bias and a line’s weight. We can’t change the activation, ideally, because that’s established by whatever input the neuron has been given. But we can change a neuron’s bias and a line’s weight. The concept of backpropagation is basically to change biases (how much you need for an activation) and weights (how seriously you take the information coming from a specific neuron) until you have the perfect (or almost perfect) biases and weights to get everything right.
Finally...
Neural networks have great applications in the world. Deep learning is basically a cool way of saying it. We’re able to beat world renowned professionals in games (I recommend the AlphaGo documentary), predict forex and stock market changes, weather forecast, recognise faces in pictures (if you’ve ever wondered how they do that), recommend pictures and videos, and oh, that Nigerian Prince, he’s straight to your spam now. All by bringing 1’s, 0’s and everything in between, and pinching them to learn.
And that’s it! We know, at least at a fundamental basis, how neural networks work. There’s a lot more to this. How does the sigmoid function work? How does backpropagation work? How does the system actually feel the cost function (the pinch)? But what the heck, we’re not trying to be Einstein’s here. If you are interested, I recommend 3Blue1Brown’s series on neural networks on YouTube, and many other scientific papers written on the matter.
But, if you’ve gotten this far, I respect you. I wouldn’t get this far. And now you probably know something you didn’t yesterday, or 30 minutes ago. Go tell your parents and brother or impress your partner. Or, just sit comfortable with that new knowledge. There's nothing wrong with a bit of new knowledge everyday :)

Please sign in
If you are a registered user on Laidlaw Scholars Network, please sign in