Enumeration, Symmetry and Classification of Fractal Carpets.
Fractal geometry is a relatively new subject in mathematics that began to pick up interest in the 1970's-1980's. It looks into studying complicated mathematical structures that have detail at arbitrarily fine scales, which means they cannot be studied by classical methods used in maths, such as calculus. As the field has developed over the last few decades, its interest has grown exponentially, with scientists, economists, mathematicians and even artists seeing the beauty and potential of this subject. For this blog post I have split it up into sections to speak a little about my research project this summer, and also speak a little about fractal geometry and it's applications.
Summer Research Project
Enumeration and symmetry:
My 5 week research project looked into a type of fractals called fractals carpets. These are fractals made from a square or rectangular construction. First, we obtain a unit square and split it into an mxm grid, where m is an integer (whole number). We then choose a selection of those squares to colour in - call this selection P. We then `map` P onto itself. An example of this is given below. For the 2x2 grid, we have a selection, P, that gives the L shape (picture on the left). We then look at each square in P, without colouring it in, pick up the picture on the left hand side, scale it down to the same size as that square in P and place it there. This produces the picture on the right.

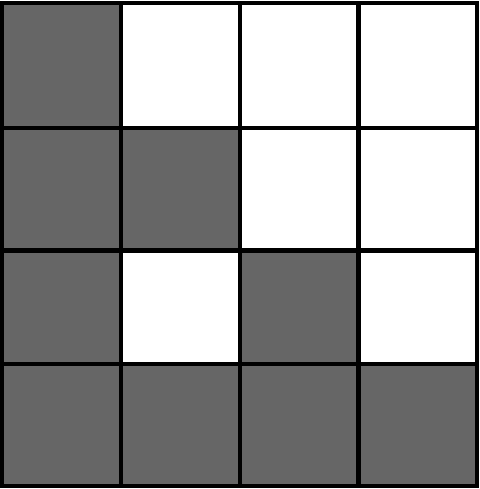
The procedure of mapping P onto itself is done infinitely many times and by standard theory in fractal geometry a unique non-empty compact attractor is obtained which often happens to be a fractal (this is written more precisely in the `fractal geometry` section).
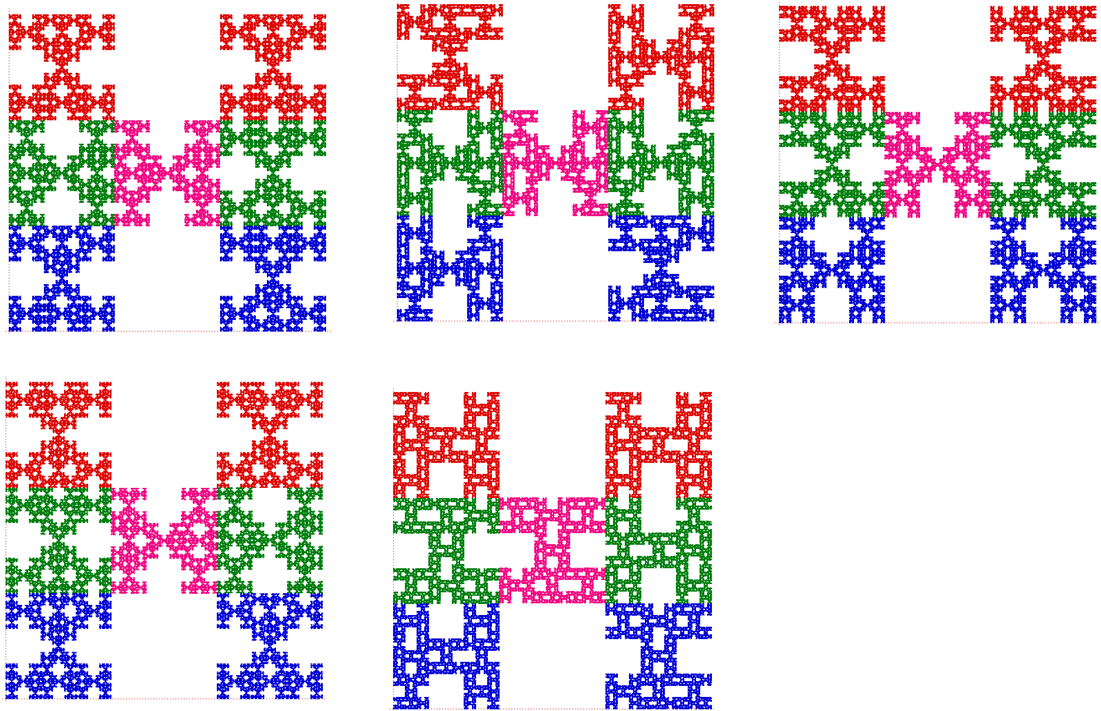
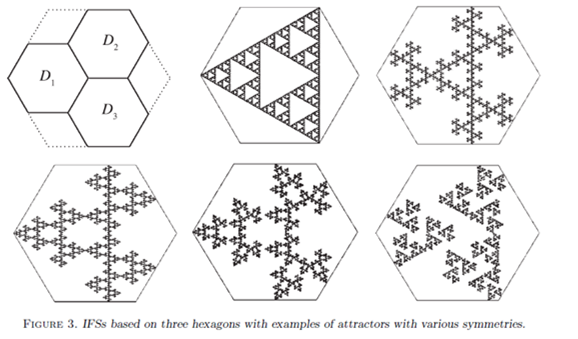
More formally, we have an Iterated function system (IFS) of similarities, mapping the unit square onto one of the squares of the mxm grid. In the first two weeks of the project, the focus was to look into how many possible attractors (often fractals) arise in a given P pattern (an example is the left picture above on the 2 x 2 grid). There are 8^3 possible IFS's for the above picture to the left, as each square in P has 8 possible symmetries (leave it the same, rotate it, reflect it diagonally or a combination of these - the picture on the right shows no rotation or reflection being induced). Each IFS has one attractor however some of the 8^3=512 IFSs share the same attractor - this occurs when the attractor has symmetry (e.g. 90 degree rotation or horizontal reflection). A method in group theory developed by Kenneth J. Falconer & John J. O'connor [1] can be used to count the number of attractors of each type of symmetry, and thus we can obtain the number of possible attractors for a given pattern P. This does not need to be a square and can be extended to various other situations. Below is a picture showing this done for a hexagon construction. This is taken from the previously referenced research paper [1]:
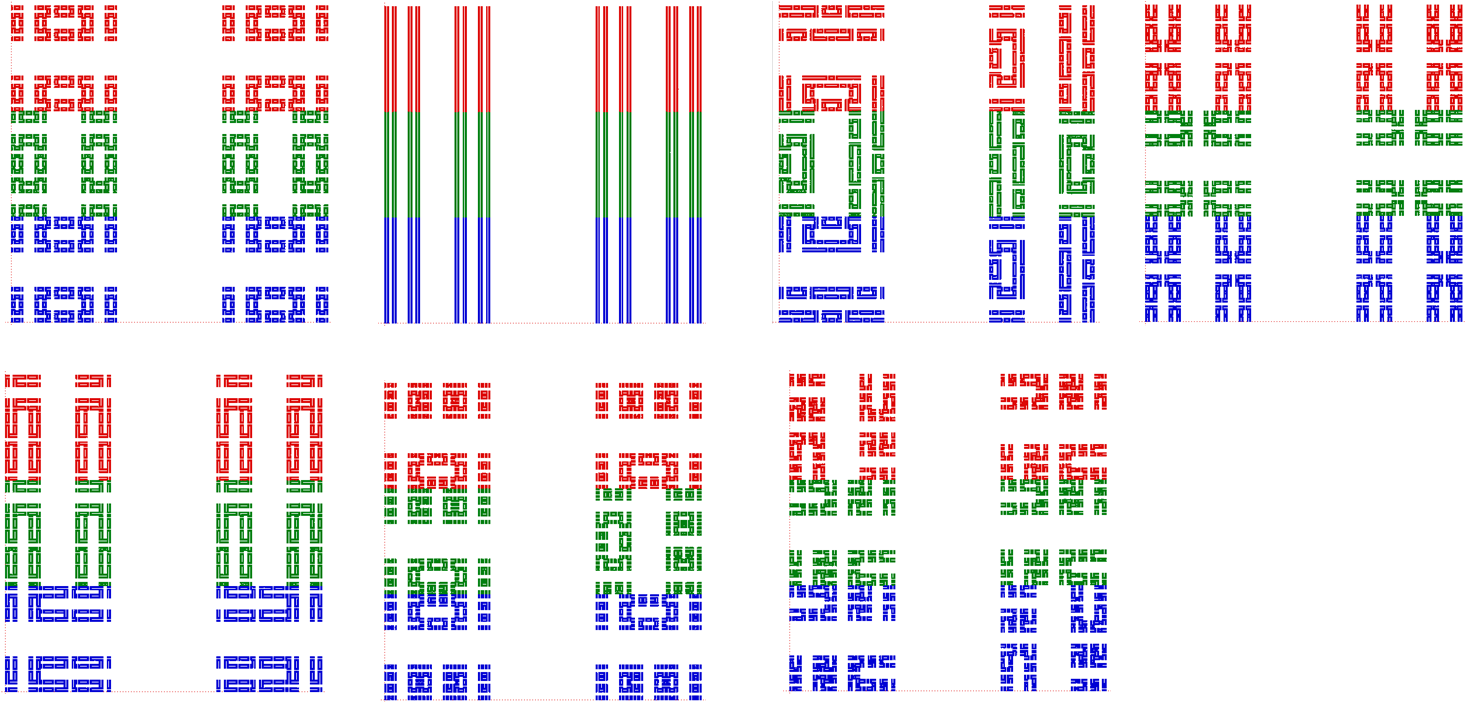
This part of the research project had some challenges. The first day I had misinterpreted some information and ended up looking at an incorrect problem. This was quickly corrected by arranging a call for the next morning. There was a number of results in the paper I had to use to study various patterns, and it took a while to see the link between these results and the symmetries they were counting. I achieved this by being patience with myself and looking over it keenly over a few days. As I needed to progress with the project as well, I managed my time so I could consider this problem while also applying the techniques to various examples. Mid-way through the first week I had successful completed some examples and understood my problem. Below I have included some pictures I created on MacTutor (pure maths software, developed in St. Andrews University) which relates directly to two of the examples I looked in detail with.


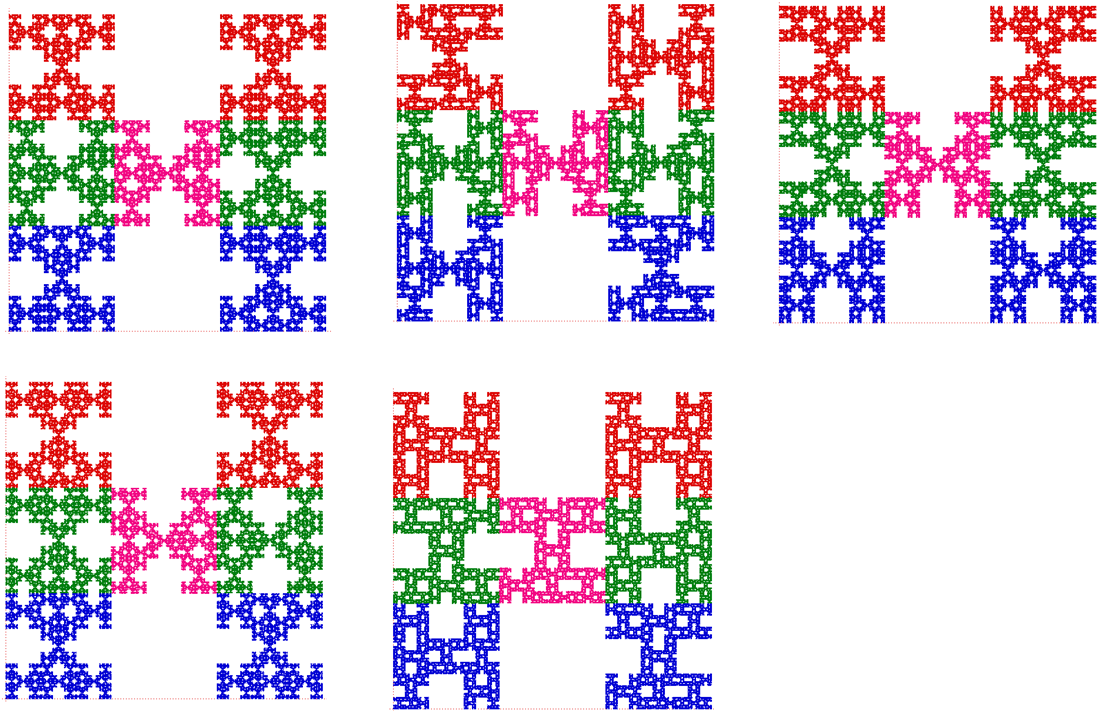
Topology & Classification:
For the remainder of the project I looked into the connectivity of some classes of fractal squares. To get an understanding of this idea I was given several research papers to read through to get the gist. These were quite dense and difficult to understand, but did succeed in giving me a deeper appreciation in what studying pure mathematics & fractal geometry is all about. Some of the papers I looked at spoke about a class of fractals know as labyrinth fractals. They initially defined a connected class of IFSs (called a labyrinth set), proved the properties work at all stages of the construction which thus implies, by a common result in topology [2], the attractor is also connected. They then looked at various other results, such as labyrinth fractals being dendrites/trees (idea in graph theory). After looking at these papers, I investigated various square constructions and how various conditions changed their connectivity (e.g. what squares need to be shaded to be diagonally connected to adjacent squares, how does rotations/reflections of some of the similarities in the IFS affect the connectivity of the attractor, etc.).
I was then asked to come up with some classes of IFS and do a couple of proofs similar to some of the ones in the research papers. I learned how to condense my work with the help of a model proof given by my supervisor.
Fractal Geometry & it's applications
A fascinating subject with a lot of potential. I wish to now mention a couple core ideas in fractal geometry and then some of it's applications, although I will not go into too much detail. For the interested reader I recommend Kenneth's books, "Fractal Geometry: Mathematical Foundations & Applications" [3] for those with a strong maths background and, "Fractals: A very short Introduction" [4] for those without a maths background. They're also various good resources online.
Some fractal geometry theory:
To start with I will mention more formally something mentioned in the previous section. An Iterated function system is a finite set of contractions, I={f1,...,fn} which has a unique, non-empty, compact attractor as mentioned above, namely F=Ui {fi(F)} . This is often a fractal.
Fractals are studied in various different ways. One way to do this is finding their fractal dimension. This is not like the typical definition of dimension, although has some similarities. They're two main ones, namely box-counting dimension and Hausdorff dimension. The dimension of a given fractal can tell us various things about the fractal (e.g. a fractal with a non-zero Hausdorff dimension less than 1 is totally disconnected), however it is possible for two fractals to have the same dimension, so other properties such as connectivity are useful in studying them.
Fractal geometry is not limited to a 2 dimension construction. There are many papers on multi-fractals, in which fractals are in many dimensions (see Kenneth's website for some 3D fractal movies [5]; link). The process for generating fractals can also be random, which can be useful when looking at applications like Brownian motion (useful in statistics).
Applications:
Fractal geometry has a wide range of applications in applied and pure maths but also in entirely different disciplines.
For pure maths fractal geometry gives rise to some nature groups. It also has a connection with dynamical systems (e.g. repellers) and number theory (e.g. continued fractions). See Kenneth's book [3] for more details.
In applied maths and the sciences, it has been used in fluid dynamics, cloud formation, astronomy (e.g. galaxy formation), medicine (e.g. looking at ECG's), financial maths (e.g. stochastic processes, looking at the stock market), and physics; see Kenneth's books [3],[4]. Physics in particular has recently published a paper on the Hausdorff dimension of electrons [6] and rearranged electrons in a fractal like shape [7] as shown below (picture is from [7]),

Acknowledgements
I would like to thank the team of the Laidlaw Foundation and Lord Laidlaw himself for giving me the opportunity to be part of this fantastic program. I wish to also thank my supervisor, Professor Kenneth J. Falconer, for his patience and dedication in helping me through this research project.
References
[1] Kenneth J. Falconer & John J. O'connor, "Symmetry & Enumeration of self-similar fractals", doi:10.1112/blms/bdl031
[2] Claude Berge, 2010. Topological Spaces. 1963 edition. New York, USA: Dover Publications Inc. (p. 98)
[3] Kenneth J. Falconer, 2014. Fractal Geometry: Mathematical Foundations & Applications. 3rd edition. Sussex, UK: John Wiley & Sons, Ltd.
[4] Kenneth J. Falconer, 2013. Fractals: A very short Introduction. Great Clarendon Street, Oxford, UK: OXFORD University Press
[5] Kenneth J. Falconer, URL - "http://www.mcs.st-and.ac.uk/~kenneth/movies.html", accessed 07/2020
[6] Kempkes, S.N., Slot, M.R., Freeney, S.E. et al. Design and characterization of electrons in a fractal geometry. Nature Phys 15, 127–131 (2019). https://doi.org/10.1038/s41567-018-0328-0
[7] phys.org. 2018. Physicists build fractal shape out of electrons. [ONLINE] Available at: https://phys.org/news/2018-11-physicists-fractal-electrons.html. [Accessed 7 July 2020].




Please sign in
If you are a registered user on Laidlaw Scholars Network, please sign in